DNN에서 Convolutional 및 FC Layers에 대한 가중치(Weight)가 특정 방식으로 초기화(Initializing).
ResNet 네트워크(https://github.com/pytorch/vision/blob/master/torchvision/models/resnet.py)
가중치를 초기화하기 위한 PyTorch 코드
n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
m.weight.data.normal_(0, math.sqrt(2. / n))- 가중치는 평균이 0인 정규 분포와 필터 커널 차원의 함수인 표준 편차를 사용하여 초기화됩니다.
- 이것은 네트워크 계층의 출력 분산이 사라지거나 폭발하는 것, 즉 매우 커지는 대신 합리적인 한계 내에서 경계를 유지하도록 하기 위해 수행됩니다.
- 이 초기화 방법은 Kaiming He et al.의 다음 논문에 자세히 설명되어 있습니다.
Section 1: Convolution을 Matrix Multiplication으로 구현
Section 2: Forward Pass (Without Bias)
Section 3: Forward Pass (With Bias)
Section 4: Other Rectifiers
- tanh 및 Sigmoid 함수와 같이 일반적으로 사용되는 기타 rectifiers(정류기: 바꿔주는 장치)를 고려합니다.
Section 1: Convolution을 Matrix Multiplication으로 구현

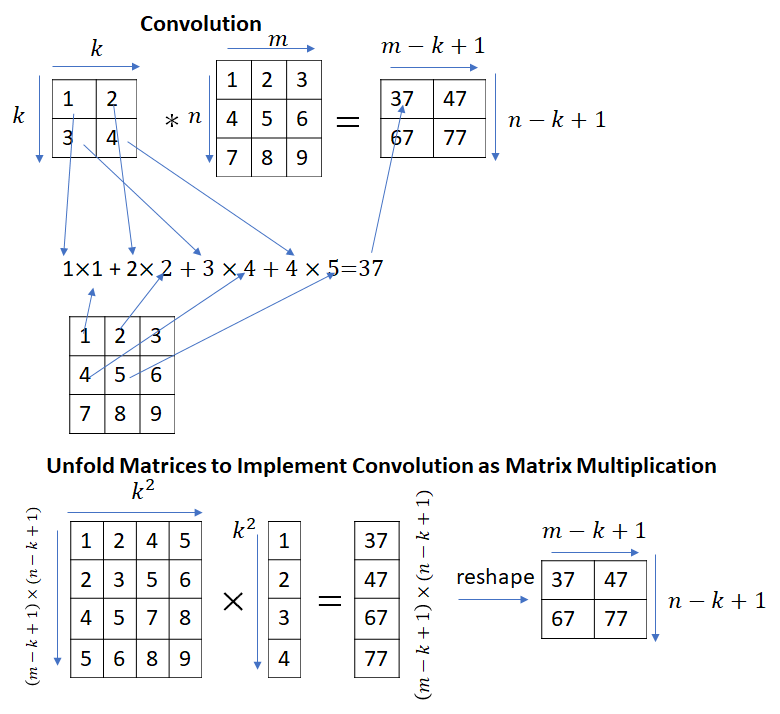
컨볼루션과 행렬 곱셈은 다른 연산입니다. 행렬 곱셈을 사용하여 컨볼루션을 구현하는 방법은 입력 행렬(또는 커널 행렬)을 적절하게 펼치면 행렬 곱셈으로 컨볼루션을 구현할 수 있습니다.
입력 행렬을 펼치고 행렬 곱셈으로 상관 관계를 구현하는 파이썬 코드
from scipy import signal
from scipy import misc
import numpy as np
from numpy import zeros
def unfold_matrix(X, k):
n, m = X.shape[0:2]
xx = zeros(((n - k + 1) * (m - k + 1), k**2))
row_num = 0
def make_row(x):
return x.flatten()
for i in range(n- k+ 1):
for j in range(m - k + 1):
#collect block of m*m elements and convert to row
xx[row_num,:] = make_row(X[i:i+k, j:j+k])
row_num = row_num + 1
return xx
w = np.array([[1, 2, 3], [4, 5, 6], [-1, -2, -3]], np.float32)
#x = np.random.randn(5,5)
x = np.array([[-0.21556299, -0.11002319, -0.3499612, 1.49290769, -0.50435978],
[ 0.06348409, 0.66873375, 0.14251138, -1.6414004 , -0.91561852],
[-2.52451962, -1.97544675, -0.24609529, -1.11489934, -1.44793437],
[ 1.26260575, -0.62047366, 0.12274525, 0.25200227, -0.83925847],
[-1.54336488, -0.05100702, 0.36608208, 0.51712927, -0.97133877],
[-1.54336488, -0.05100702, 0.36608208, 0.51712927, -0.97133877]])
n, m = x.shape[0:2]
k = w.shape[0]
y = signal.correlate2d(x, w, mode='valid')
x_unfolded = unfold_matrix(x, k)
w_flat = w.flatten()
yy = np.matmul(x_unfolded, w_flat)
yy = yy.reshape((n-k+1, m-k+1))
print(yy)
# verify yy = y
Section 2: Forward Pass (Without Bias)

네트워크가 깊어짐에 따라 네트워크 출력의 분산이 사라지거나 과도하게 커지는 대신 경계를 유지하도록 가중치에 대한 적절한 분산을 선택하는 것
# number of layers
num_layers = 10
class layer(object):
def __init__(self, _m, _n):
#n: filter size (width)
#m: filter size (height)
self.m = _m
self.n = _n
self.activation = 'relu'
#self.activation = 'tanh'
#self.activation = 'sigmoid'
def sigmoid(self, x):
return 1 / (1 + np.exp(-x))
def forward(self, x, use_bias = False):
#x is a row vector
self.W = np.random.normal(0, np.sqrt(2.0/self.m), (self.m,self.n))
self.b = np.random.normal(0, np.sqrt(2.0/num_layers), self.n)
# self.b = 1. - 2*np.random.rand(1, 5)
self.y = np.dot(x, self.W)
if (use_bias):
self.y = self.y + self.b
if (self.activation == 'relu'):
self.a = np.maximum(0., self.y)
if (self.activation == 'tanh'):
self.a = np.tanh(self.y)
if (self.activation == 'sigmoid'):
self.a = self.sigmoid(self.y)
return self.a, self.y
layers = []
# even numbered layers have a 5*10 weight matrix
# odd numbered layers have a 10*5 weight matrix
for i in range(num_layers):
layers.append(layer(5 if(i % 2 == 0) else 10, 10 if(i % 2 == 0) else 5))
num_trials = 100000
# records the network output (activations of the last layer)
a = np.zeros((num_trials, 5))
# records the network input
i = np.zeros((num_trials, 5))
# record the activations
y = np.zeros((num_trials, 5))
for trial in range(0,num_trials):
# input to the network is uniformly distributed numbers in (0,1). E(x) != 0.
# Note that the distribution of the input is different from the distribution of the weights.
x = 3*np.random.rand(1, 5)
i[trial, :] = x
for layer_no in range(0,num_layers):
x, y_ = layers[layer_no].forward(x, False)
a[trial, :] = x
y[trial, :] = y_
#E(x^2) (expected value of the square of the input)
E_x2 = np.mean(np.multiply(i,i), 0)
# E(a^2) (expected value of the square of the activations of the last layer)
E_a2 = np.mean(np.multiply(a,a), 0)
# verify E_a2 ~ E_x2
# var(y): Variance of the output before applying activation function
Var_y = np.var(y,0)
# verify Var_y ~ 2*E_a2
Section 3: Forward Pass (With Bias)

가중치와 편향을 다음과 같이 초기화합니다.
self.W = np.random.normal(0, np.sqrt(2.0/self.m), (self.m,self.n))
self.b = np.random.normal(0, np.sqrt(2.0/num_layers), self.n)
네트워크를 실행하는 동안 use_bias = True로 설정합니다.
for layer_no in range(0,num_layers):
x, y_ = layers[layer_no].forward(x, True)
Backward Pass
Backward Pass를 고려할 때 초기화 방법을 수정할 필요가 없다는 것이 밝혀졌습니다. 이는 역방향 패스 동안 완전히 연결된 컨볼루션 레이어를 통해 그라디언트를 전파하면 차원이 약간 다른 행렬 곱셈과 컨볼루션이 발생하기 때문입니다.
Section 4: Other Rectifiers
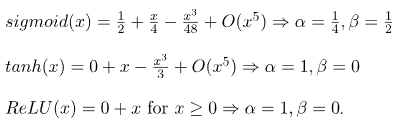
시그모이드 활성화 함수의 크기를 조정하고 편향을 추가하여 수정할 수 있습니다.
해해야 할 핵심은 정규 분포를 샘플링하여 가중치를 초기화하는 표준 방법 u=0이다.
ReLU 활성화 함수를 위해 설계되었으며 tanh 활성화에는 잘 작동하지만 S자형에는 잘 작동하지 않습니다.
참고: TELESENS. Ankur
'📁 AI & Bigdata > AI & ML & DL' 카테고리의 다른 글
| [DL] TensorFlow- 심층신경망 모델 코드 구현 (0) | 2022.08.19 |
|---|---|
| [DL] Faster R-CNN 네트워크 세부 구성 (0) | 2022.08.18 |
| [DL] CNN 분류 성능 높이기/ 데이터 증가, Mix Image (0) | 2022.08.09 |
| [DL] YOLO- 라즈베리 파이를 이용한 Object Recognition, Text Recognition -딥러닝 기술 YOLO 활용 (0) | 2022.08.09 |
| [DL] Faster R-CNN (0) | 2022.08.02 |
